| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 3.1 | Example 1 & 2 (Before Exercise 3.2) | Exercise 3.2 |
| Example 3 & 4 (Before Exercise 3.3) | Exercise 3.3 | |
Chapter 3 Coordinate Geometry
Welcome to the solutions for Chapter 3: Coordinate Geometry. This vital chapter lays the essential groundwork for visualizing algebraic concepts and analyzing geometric figures within a structured framework. It introduces the powerful Cartesian coordinate system, a fundamental tool developed by René Descartes that elegantly bridges the gap between algebra and geometry. Mastering the vocabulary and techniques presented here is absolutely crucial for navigating more advanced topics involving graphs, functions, and geometric transformations. These solutions aim to provide crystal-clear explanations and guide you through the core principles of locating points in a two-dimensional plane.
The core of this chapter revolves around understanding the architecture of the Cartesian plane. Our solutions carefully dissect its components:
- The horizontal number line, designated as the x-axis.
- The vertical number line, designated as the y-axis.
- Their unique point of intersection, known as the origin, which corresponds to the coordinates $(0, 0)$.
- The four distinct regions, termed quadrants, created by the intersection of these axes.
A key aspect detailed in the solutions is the established sign convention for coordinates $(x, y)$ within each quadrant, which is essential for accurate plotting and interpretation:
- Quadrant I: Both coordinates are positive $(+, +)$.
- Quadrant II: The x-coordinate is negative, and the y-coordinate is positive $(-, +)$.
- Quadrant III: Both coordinates are negative $(-,-)$.
- Quadrant IV: The x-coordinate is positive, and the y-coordinate is negative $(+,-)$.
The solutions thoroughly explain the meaning of the two values in an ordered pair $(x, y)$ that define a point's location. The first value, the x-coordinate or abscissa, represents the directed perpendicular distance of the point from the y-axis. The second value, the y-coordinate or ordinate, represents the directed perpendicular distance from the x-axis. Emphasis is placed on correctly interpreting these distances and their signs. A primary skill developed through these solutions is the ability to accurately plot points on graph paper when provided with their coordinates, such as $(-3, 4)$ or $(5, -2)$.
The practical process of plotting is broken down into simple, sequential steps: always begin at the origin $(0,0)$; first, move horizontally along the x-axis according to the abscissa's value (right for positive $x$, left for negative $x$); second, move vertically, parallel to the y-axis, according to the ordinate's value (up for positive $y$, down for negative $y$). Conversely, the solutions also equip you with the skill to determine the coordinates of a point already marked on the Cartesian plane by observing its position relative to the x-axis and y-axis and applying the sign conventions. Exercises often involve identifying if a point like $(0, 5)$ lies on an axis (in this case, the y-axis) or in a specific quadrant. While seemingly basic, this precise understanding of the coordinate system's structure and the mechanics of plotting and reading points forms an indispensable foundation for future mathematical explorations, particularly in graphing linear equations and delving deeper into analytical geometry.
Exercise 3.1
Question 1. How will you describe the position of a table lamp on your study table to another person?
Answer:
To describe the position of a table lamp on a study table to another person, we can use the principles of a coordinate system, similar to how points are located on a graph.
Method of Description:
1. Consider the table as a plane: First, we imagine the flat surface of the study table as a two-dimensional plane.
2. Establish a reference point (Origin): To describe a position, we need a fixed starting point. We can choose any corner of the table as our reference point or origin. Let's assume we are sitting at the table, and we choose the front-left corner as the origin (0, 0).
3. Define the axes: The two edges of the table that meet at our chosen corner will serve as our axes.
- The front edge (the one closest to you) can be considered the x-axis.
- The left edge can be considered the y-axis.
4. Measure the distances: Now, we measure the perpendicular distance of the lamp's base from these two edges.
- Measure the distance of the lamp from the left edge (the y-axis). This measurement will give us the x-coordinate.
- Measure the distance of the lamp from the front edge (the x-axis). This measurement will give us the y-coordinate.
5. State the position as an ordered pair: We can now describe the position of the lamp using an ordered pair of coordinates (x, y).
Example:
Let's say we measure the distances and find that:
- The distance of the lamp from the left edge is 30 cm.
- The distance of the lamp from the front edge is 20 cm.
We can then tell the other person:
"Considering the front-left corner of the table as the origin, the front edge as the x-axis, and the left edge as the y-axis, the position of the table lamp is at the point (30 cm, 20 cm)."
This provides a precise and unambiguous description of the lamp's location on the table.
Question 2. (Street Plan) : A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North - South direction and another in the East - West direction. Each cross street is referred to in the following manner : If the 2nd street running in the North - South direction and 5th in the East - West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:
(i) how many cross - streets can be referred to as (4, 3).
(ii) how many cross - streets can be referred to as (3, 4).
Answer:
Solution:
First, we will draw a model of the city's street plan based on the description. The plan can be represented as a Cartesian coordinate system.
- The main North-South road can be considered the y-axis.
- The main East-West road can be considered the x-axis.
- The five streets running parallel to the North-South road can be thought of as vertical lines (like x=1, x=2, ...).
- The five streets running parallel to the East-West road can be thought of as horizontal lines (like y=1, y=2, ...).
The convention for referring to a cross-street is (North-South street number, East-West street number). This is equivalent to an ordered pair (x-coordinate, y-coordinate), where the North-South street determines the horizontal position and the East-West street determines the vertical position.
Now, using this model and convention, we can find the answers to the questions.
(i) how many cross-streets can be referred to as (4, 3).
The coordinate (4, 3) refers to a unique intersection point defined by:
- The 4th street running in the North-South direction.
- The 3rd street running in the East-West direction.
In a coordinate system, a specific pair of coordinates like (4, 3) refers to one and only one point. On the street plan, there will be exactly one intersection where the 4th North-South street crosses the 3rd East-West street.
Therefore, there is only one cross-street that can be referred to as (4, 3).
(ii) how many cross-streets can be referred to as (3, 4).
Similarly, the coordinate (3, 4) refers to a unique intersection point defined by:
- The 3rd street running in the North-South direction.
- The 4th street running in the East-West direction.
This is a different, but also unique, intersection point on the street plan. There is only one place where the 3rd North-South street crosses the 4th East-West street.
Therefore, there is only one cross-street that can be referred to as (3, 4).
Example 1 & 2 (Before Exercise 3.2)
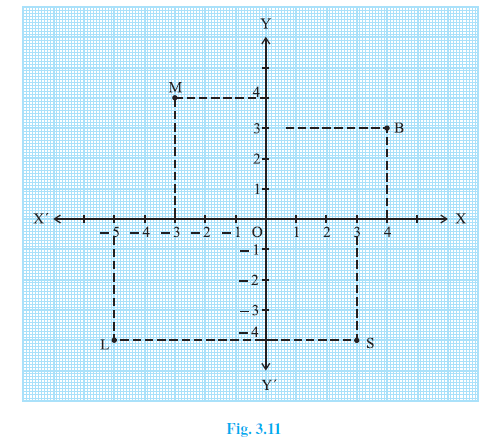
Example 1. See the Fig. 3.11 and complete the following statements:
(i) The abscissa and the ordinate of the point B are _ _ _ and _ _ _, respectively. Hence, the coordinates of B are (_ _, _ _).
(ii) The x-coordinate and the y-coordinate of the point M are _ _ _ and _ _ _, respectively. Hence, the coordinates of M are (_ _, _ _).
(iii) The x-coordinate and the y-coordinate of the point L are _ _ _ and _ _ _, respectively. Hence, the coordinates of L are (_ _, _ _).
(iv) The x-coordinate and the y-coordinate of the point S are _ _ _ and _ _ _, respectively. Hence, the coordinates of S are (_ _, _ _).
Answer:
By observing the positions of the points B, M, L, and S on the Cartesian plane in Fig. 3.11, we can determine their coordinates.
(i) The abscissa and the ordinate of the point B are 4 and 3, respectively. Hence, the coordinates of B are (4, 3).
Reason: Point B is 4 units to the right of the y-axis (positive x-direction) and 3 units above the x-axis (positive y-direction).
(ii) The x-coordinate and the y-coordinate of the point M are -3 and 4, respectively. Hence, the coordinates of M are (-3, 4).
Reason: Point M is 3 units to the left of the y-axis (negative x-direction) and 4 units above the x-axis (positive y-direction).
(iii) The x-coordinate and the y-coordinate of the point L are -5 and -4, respectively. Hence, the coordinates of L are (-5, -4).
Reason: Point L is 5 units to the left of the y-axis (negative x-direction) and 4 units below the x-axis (negative y-direction).
(iv) The x-coordinate and the y-coordinate of the point S are 3 and -4, respectively. Hence, the coordinates of S are (3, -4).
Reason: Point S is 3 units to the right of the y-axis (positive x-direction) and 4 units below the x-axis (negative y-direction).
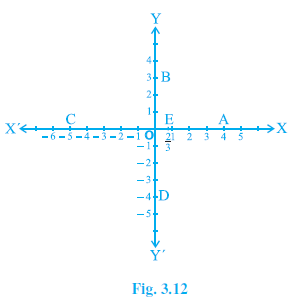
Example 2. Write the coordinates of the points marked on the axes in Fig. 3.12.
Answer:
Solution:
To find the coordinates of points lying on the axes, we use the following rules:
- Any point on the x-axis has a y-coordinate of 0. Its coordinates are in the form $(x, 0)$.
- Any point on the y-axis has an x-coordinate of 0. Its coordinates are in the form $(0, y)$.
By observing Fig. 3.12, we can determine the coordinates of each marked point:
Point A:
Point A lies on the positive x-axis at a distance of 4 units from the origin. Therefore, its y-coordinate is 0 and its x-coordinate is 4.
The coordinates of point A are (4, 0).
Point B:
Point B lies on the positive y-axis at a distance of 3 units from the origin. Therefore, its x-coordinate is 0 and its y-coordinate is 3.
The coordinates of point B are (0, 3).
Point C:
Point C lies on the negative x-axis at a distance of 5 units from the origin. Therefore, its y-coordinate is 0 and its x-coordinate is -5.
The coordinates of point C are (-5, 0).
Point D:
Point D lies on the negative y-axis at a distance of 4 units from the origin. Therefore, its x-coordinate is 0 and its y-coordinate is -4.
The coordinates of point D are (0, -4).
Point E:
Point E lies on the positive x-axis at a distance of $\frac{2}{3}$ units from the origin. Therefore, its y-coordinate is 0 and its x-coordinate is $\frac{2}{3}$.
The coordinates of point E are ($\frac{2}{3}$, 0).
Exercise 3.2
Question 1. Write the answer of each of the following questions:
(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
(ii) What is the name of each part of the plane formed by these two lines?
(iii) Write the name of the point where these two lines intersect.
Answer:
(i) The name of the horizontal line is the x-axis, and the name of the vertical line is the y-axis.
(ii) The name of each part of the plane formed by these two lines (x-axis and y-axis) is a Quadrant. (There are four quadrants: Quadrant I, Quadrant II, Quadrant III, and Quadrant IV).
(iii) The name of the point where these two lines intersect is the Origin.
Question 2. See Figure given below, and write the following:
(i) The coordinates of B.
(ii) The coordinates of C.
(iii) The point identified by the coordinates (–3, –5).
(iv) The point identified by the coordinates (2, – 4).
(v) The abscissa of the point D.
(vi) The ordinate of the point H.
(vii) The coordinates of the point L.
(viii) The coordinates of the point M.

Answer:
(i) The coordinates of B:
To find the coordinates of point B, we look at its position relative to the axes. Draw a perpendicular line from B to the x-axis; it meets the x-axis at -5. Draw a perpendicular line from B to the y-axis; it meets the y-axis at 2. The x-coordinate (abscissa) is -5 and the y-coordinate (ordinate) is 2.
Therefore, the coordinates of B are (-5, 2).
(ii) The coordinates of C:
Follow the same process for point C. A perpendicular line from C meets the x-axis at 5. A perpendicular line from C meets the y-axis at -5. The x-coordinate is 5 and the y-coordinate is -5.
Therefore, the coordinates of C are (5, -5).
(iii) The point identified by the coordinates (–3, –5):
To find the point corresponding to (–3, –5), we start at the origin (0, 0). Move 3 units along the negative x-axis (to the left) to reach x = -3. From there, move 5 units along the negative y-axis direction (downwards) to reach y = -5. The point located at this position in the figure is E.
Therefore, the point identified by (–3, –5) is E.
(iv) The point identified by the coordinates (2, – 4):
Start at the origin (0, 0). Move 2 units along the positive x-axis (to the right) to reach x = 2. From there, move 4 units along the negative y-axis direction (downwards) to reach y = -4. The point located at this position in the figure is G.
Therefore, the point identified by (2, – 4) is G.
(v) The abscissa of the point D:
First, find the coordinates of point D. A perpendicular from D meets the x-axis at 6 and the y-axis at 2. So, the coordinates of D are (6, 2). The abscissa is defined as the x-coordinate of a point.
Therefore, the abscissa of the point D is 6.
(vi) The ordinate of the point H:
First, find the coordinates of point H. A perpendicular from H meets the x-axis at -5 and the y-axis at -3. So, the coordinates of H are (-5, -3). The ordinate is defined as the y-coordinate of a point.
Therefore, the ordinate of the point H is -3.
(vii) The coordinates of the point L:
Observe that point L lies directly on the positive y-axis. Any point lying on the y-axis always has an x-coordinate of 0. The point L is located at the mark '5' on the y-axis.
Therefore, the coordinates of the point L are (0, 5).
(viii) The coordinates of the point M:
Observe that point M lies directly on the negative x-axis. Any point lying on the x-axis always has a y-coordinate of 0. The point M is located at the mark '-3' on the x-axis.
Therefore, the coordinates of the point M are (-3, 0).
Example 3 & 4 (Before Exercise 3.3)
Example 3. Locate the points (5, 0), (0, 5), (2, 5), (5, 2), (–3, 5), (–3, –5), (5, –3) and (6, 1) in the Cartesian plane.
Answer:
Solution:
To locate these points in the Cartesian plane, we use a set of perpendicular axes: the horizontal x-axis and the vertical y-axis. The position of each point $(x, y)$ is determined by its x-coordinate (abscissa) and y-coordinate (ordinate).
- The x-coordinate tells us the horizontal distance from the y-axis (positive to the right, negative to the left).
- The y-coordinate tells us the vertical distance from the x-axis (positive upwards, negative downwards).
Let's assign a variable to each coordinate pair for easier reference:
- A = (5, 0)
- B = (0, 5)
- C = (2, 5)
- D = (5, 2)
- E = (–3, 5)
- F = (–3, –5)
- G = (5, –3)
- H = (6, 1)
The location of each point is shown on the graph below.
Description of Each Point's Location:
- Point A(5, 0): This point has a y-coordinate of 0, so it lies on the x-axis at a distance of 5 units to the right of the origin.
- Point B(0, 5): This point has an x-coordinate of 0, so it lies on the y-axis at a distance of 5 units above the origin.
- Point C(2, 5): This point is in Quadrant I because both its x and y coordinates are positive.
- Point D(5, 2): This point is also in Quadrant I. Note that it is a different point from C(2, 5).
- Point E(–3, 5): This point is in Quadrant II because its x-coordinate is negative and its y-coordinate is positive.
- Point F(–3, –5): This point is in Quadrant III because both its x and y coordinates are negative.
- Point G(5, –3): This point is in Quadrant IV because its x-coordinate is positive and its y-coordinate is negative.
- Point H(6, 1): This point is in Quadrant I because both coordinates are positive.
Example 4. Plot the following ordered pairs (x, y) of numbers as points in the Cartesian plane. Use the scale 1 cm = 1 unit on the axes.
| x | – 3 | 0 | – 1 | 4 | 2 |
| y | 7 | –3.5 | – 3 | 4 | – 3 |
Answer:
Solution:
We are given a table of x and y values, which represent a set of ordered pairs (points) to be plotted on the Cartesian plane. The points are:
- A: (-3, 7)
- B: (0, -3.5)
- C: (-1, -3)
- D: (4, 4)
- E: (2, -3)
We will draw the Cartesian plane with the x-axis and y-axis and plot each point according to its coordinates. We will use a scale of 1 cm = 1 unit on both axes.
Steps for Plotting the Points:
- Point A (-3, 7): Start at the origin (0,0). Move 3 units to the left along the x-axis (to -3), and then move 7 units upwards, parallel to the y-axis. Mark this point as A.
- Point B (0, -3.5): The x-coordinate is 0, so the point lies on the y-axis. Start at the origin and move 3.5 units downwards along the y-axis (to -3.5). Mark this point as B.
- Point C (-1, -3): Start at the origin. Move 1 unit to the left along the x-axis (to -1), and then move 3 units downwards, parallel to the y-axis. Mark this point as C.
- Point D (4, 4): Start at the origin. Move 4 units to the right along the x-axis (to 4), and then move 4 units upwards, parallel to the y-axis. Mark this point as D.
- Point E (2, -3): Start at the origin. Move 2 units to the right along the x-axis (to 2), and then move 3 units downwards, parallel to the y-axis. Mark this point as E.
The final plot showing all the points is presented below.
Exercise 3.3
Question 1. In which quadrant or on which axis do each of the points (– 2, 4), (3, – 1), (– 1, 0), (1, 2) and (– 3, – 5) lie? Verify your answer by locating them on the Cartesian plane.
Answer:
Solution:
To determine the quadrant or axis for each point, we look at the signs of its x and y coordinates.
- Quadrant I: x > 0, y > 0 (+, +)
- Quadrant II: x < 0, y > 0 (-, +)
- Quadrant III: x < 0, y < 0 (-, -)
- Quadrant IV: x > 0, y < 0 (+, -)
- On x-axis: y = 0
- On y-axis: x = 0
Analysis of Each Point:
- (– 2, 4): The x-coordinate is negative (–2) and the y-coordinate is positive (4). This point lies in Quadrant II.
- (3, – 1): The x-coordinate is positive (3) and the y-coordinate is negative (–1). This point lies in Quadrant IV.
- (– 1, 0): The y-coordinate is 0. This point lies on the negative x-axis.
- (1, 2): The x-coordinate is positive (1) and the y-coordinate is positive (2). This point lies in Quadrant I.
- (– 3, – 5): The x-coordinate is negative (–3) and the y-coordinate is negative (–5). This point lies in Quadrant III.
Verification by Locating the Points on the Cartesian Plane:
We can now plot these points on a graph to visually verify their locations.
The plot confirms our analysis:
- (– 2, 4) is in Quadrant II.
- (3, – 1) is in Quadrant IV.
- (– 1, 0) is on the x-axis.
- (1, 2) is in Quadrant I.
- (– 3, – 5) is in Quadrant III.
Question 2. Plot the points (x, y) given in the following table on the plane, choosing suitable units of distance on the axes.
| x | – 2 | –1 | 0 | 1 | 3 |
| y | 8 | 7 | – 1.25 | 3 | – 1 |
Answer:
Solution:
We are given a table of x and y values. These values correspond to the following ordered pairs (points) that need to be plotted on a Cartesian plane:
- (-2, 8)
- (-1, 7)
- (0, -1.25)
- (1, 3)
- (3, -1)
We will draw a Cartesian plane and choose a suitable scale for the axes to accommodate all the given points. Let's use 1 unit on the grid for 1 unit of distance on both the x-axis and the y-axis.
Plotting the Points:
We will locate and mark each point on the plane:
- (-2, 8): Start at the origin, move 2 units to the left (negative x-direction), and then 8 units up (positive y-direction). This point lies in Quadrant II.
- (-1, 7): Start at the origin, move 1 unit to the left, and then 7 units up. This point also lies in Quadrant II.
- (0, -1.25): The x-coordinate is 0, so this point lies on the y-axis. We move 1.25 units down from the origin. The point -1.25 is one-quarter of the way between -1 and -2.
- (1, 3): Start at the origin, move 1 unit to the right (positive x-direction), and then 3 units up. This point lies in Quadrant I.
- (3, -1): Start at the origin, move 3 units to the right, and then 1 unit down (negative y-direction). This point lies in Quadrant IV.
The resulting graph with all the plotted points is shown below.

